domingo, 14 de fevereiro de 2010

Determinante

Em matemática, determinante é uma função que associa a cada matriz quadrada um escalar. Esta função permite saber se a matriz tem ou não inversa, pois as que não têm são precisamente aquelas cujo determinante é igual a 0.

Definição

Seja M o conjunto das matrizes com n linhas e n colunas sobre um corpo K. Pode-se provar que existe uma única função f com as seguintes propriedades:
  1. f é n-linear e alternada nas linhas das matrizes;
  2. f(In) = 1, onde In é a matriz identidade.
Esta função chama-se determinante.
O determinante de uma matriz A representa-se por |A| ou por det(A).

Propriedades

  1. O determinante também é uma função n-linear e alternada nas colunas da matriz;
  2. O determinante de uma matriz é igual ao determinante da sua transposta: det(A) = det(AT);
  3. Se uma fila (linha ou coluna) da matriz é composta de zeros, então o determinante desta matriz será zero;
  4. Se escrevermos cada elemento de uma linha ou coluna de A como soma de duas parcelas então det(A) é a soma de dois determinantes de ordem n cada um considerando como elemento daquela linha ou coluna uma das parcelas, e repetindo as demais linhas ou colunas;
  5. Se uma matriz é triangular (superior ou inferior) o seu determinante é o produto dos elementos da diagonal principal;
  6. Multiplicando uma fila (linha ou coluna) de uma matriz A por um escalar λ ∈ K, então o determinante da nova matriz é igual ao determinante de A multiplicado por λ;
  7. Se permutarmos duas linhas ou colunas de A então o determinante da nova matriz é −det(A);
  8. Se A tem duas linhas (ou colunas) iguais, então det(A) = 0;
  9. Se somarmos a uma linha (ou coluna) de A um múltiplo de outra linha (ou coluna), o determinante da nova matriz é igual ao de A;
  10. Se A e B são matriz quadradas da mesma ordem, então det(AB) = det(A).det(B);
  11. Se A é invertível, então det(A−1) = 1⁄det(A), de onde resulta que se A é invertível então det(A) ≠ 0;
  12. Se A é ortogonal, então det(A) = ±1.

Determinante de uma matriz de ordem 1

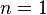O determinante da matriz A \, de ordem n = 1 \,, é o próprio número que origina a matriz. Dada uma matriz quadrada de 1ª ordem M=[a_{11}] \, temos que o determinante é o número real a_{11} \,:
det(M) = a_{11} \,.
Por exemplo:
A = ( 3 ) \, , então det(A) = 3 \, .

Determinante de matriz de ordem 2

A area do paralelogramo é o determinate da matriz formada pelos vetores que representam seus lados.
O determinante de uma matriz de segunda ordem é a diferença entre o produto dos termos da diagonal principal e o produto dos termos da diagonal secundária. Esses produtos se chamam, respectivamente, termo principal e termo secundário da matriz.
\hbox{det} \begin{pmatrix} a & b \\ c & d \end{pmatrix}=ad-bc .
Por exemplo, o determinante da matriz \begin{pmatrix} 0 & 2 \\ 1 & -1 \end{pmatrix} é dado por: 0.(-1) - 2.1 = 0 - 2 = -2 \, .

Determinante de matriz de terceira ordem

O determinante de uma matriz 3x3 é calculado através de suas diagonais.
Para calcular o determinante de matrizes de terceira ordem, utilizamos a chamada regra de Sarrus, que resulta no seguinte cálculo:
\det \begin{pmatrix} a & b & c\\ d & e & f \\ g & h & i \end{pmatrix}=(aei + dhc + gbf) - (ceg + fha + ibd) .
  • Por exemplo:
A = \begin{pmatrix} 1 & 3 & 10\\ -1 & 1 & 10 \\ 0 & 2 & 10 \end{pmatrix} \Rightarrow \begin{vmatrix} 1 & 3 & 10\\ -1 & 1 & 10 \\ 0 & 2 & 10 \end{vmatrix} \begin{vmatrix} 1 & 3\\ -1 & 1 \\ 0 & 2 \end{vmatrix}
\det(A) = ((1 . 1 . 10) + (3 . 10 . 0) + (10 . (-1) . 2)) - ((0 . 1 .10) + (2 . 10 . 1) + (10 . (-1) . 3)) \,
= (10 + 0 + (-20)) - ((0 + 20 + (-30))\,
= 0 \,

Determinantes de ordem maior ou igual a 4

Para calcularmos o determinantes de matrizes com ordem igual ou superior a quatro, podemos reduzir a sua ordem. Seja a matriz
A = \begin{pmatrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34}\\ a_{41} & a_{42} & a_{43} & a_{44}\end{pmatrix}
Desenvolvendo o determinante pela primeira linha obtemos:
\det A = a_{11} . (-1)^{1+1} . \det A_{-1,-1} + \,
a_{12} . (-1)^{1+2} . det A_{-1,-2} + \,
a_{13} . (-1)^{1+3} . det A_{-1,-3} + \,
a_{14} . (-1)^{1+4} . det A_{-1,-4} \, ,
onde A−i,−j representa a matriz obtida a partir de A, com a retirada da i-ésima linha e da j-ésima coluna. Retorna-se ao cálculo de quatro determinantes de matrizes de terceira ordem.
Então definimos o determinante de ordem n desenvolvido pela i-ésima linha:
\det \begin{vmatrix} a_{11} & a_{12} & \ldots & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n} \\ : & : & :: & :\\ a_{n-1,1} & a_{n-1,2} & \ldots & a_{n-1,n}\\ a_{n1} & a_{n2} & \ldots & a_{nn}\end{vmatrix}= \sum_{j=1}^{n} a_{ij} (-1)^{i+j} \cdot det A_{-i,-j} \, .

Cálculo de determinantes por triangularização

Tendo em vista a propriedade de que o determinante de uma matriz triangular é o seu termo principal (propriedade 5), a idéia é aplicar operações elementares sobre suas linhas, de modo a triangularizá-lo. Para isso devemos observar os efeitos que cada operação elementar pode ou não causar no valor do determinante procurado:
  • Permutar linhas troca o sinal do determinante (propriedade 7);
  • Multiplicar uma linha por um número real 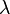\lambda \, não nulo, multiplica o determinante por 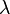\lambda \, (propriedade 6);
  • Somar a uma linha um múltiplo de outra não altera o determinante (propriedade 9).
Para triangularizar um determinante basta atentar para as possíveis compensações provocadas pelas operações elementares utilizadas e não há uma única maneira de realizar esse processo. O método é algorítmico, constituído de passos simples: a cada coluna, da primeira à penultima, deve-se obter zeros nas posições abaixo da diagonal principal. Veja o exemplo a seguir:
\begin{vmatrix} 2 & -4 & 8\\ 5 & 4 & 6 \\ -3 & 0 & 2 \end{vmatrix} L_1 \leftarrow \frac{1}{2} L_1 = 2 \cdot \begin{vmatrix} 1 & -2 & 4\\ 5 & 4 & 6 \\ -3 & 0 & 2 \end{vmatrix} L_{2} \leftarrow L_{2} - 5.L_{1} \land L_{3} \leftarrow L_{3} + 3.L_{1} = 2 \cdot \begin{vmatrix} 1 & -2 & 4\\ 0 & 14 & -14 \\ 0 & -6 & 14 \end{vmatrix} L_{2} \leftarrow \frac{1}{14} =
2 \cdot 14 \cdot \begin{vmatrix} 1 & -2 & 4\\ 0 & 1 & -1 \\ 0 & -6 & 14 \end{vmatrix} L_{3} \leftarrow L_{3} + 6.L_{2} = 2 \cdot 14 \cdot \begin{vmatrix} 1 & -2 & 4\\ 0 & 1 & -1 \\ 0 & 0 & 8 \end{vmatrix} = 2 \cdot 14 \cdot 1 \cdot 1 \cdot 8 = 224
Postado por às Nenhum comentário:

Produto de Matrizes

Em matemática, o produto de duas matrizes é definido somente quando o número de colunas da primeira matriz é igual ao número de linhas da segunda matriz. Se A é uma matriz m-por-n e B é uma matriz n-por-p, então seu produto é uma matriz m-por-p definida como AB (ou por A · B). O produto é dado por
(AB)_{ij} = \sum_{r=1}^n a_{ir}b_{rj} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj}.
para cada par i e j com 1 ≤ i ≤ m e 1 ≤ j ≤ p.

Calculando directamente a partir da definição

Matrix multiplication diagram.PNG
A figura à esquerda mostra como calcular o elemento (1,2) e o elemento (3,3) de AB se A é uma matriz 4×2, e B é uma matriz 2×3. Elementos de cada matriz são postos par a par na direcção das setas; cada par é multiplicado e os produtos são somados. A posição do número resultante em AB corresponde ao da seta e coluna que foi considerada.
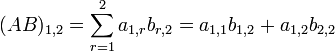
(AB)_{1,2} = \sum_{r=1}^2 a_{1,r}b_{r,2} = a_{1,1}b_{1,2}+a_{1,2}b_{2,2}
(AB)_{3,3} = \sum_{r=1}^2 a_{3,r}b_{r,3} = a_{3,1}b_{1,3}+a_{3,2}b_{2,3}

Propriedades

  • Multiplicação de matrizes não é em geral comutativa, ou seja, AB ≠ BA(exceto em casos especiais). Eis um contra-exemplo:
\left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right] \cdot \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right]= \left[\begin{array}{cc} 0 & 1 \\ 2 & 0 \end{array}\right]
\left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] \cdot \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right]= \left[\begin{array}{cc} 0 & 2 \\ 1 & 0 \end{array}\right]
  • Embora multiplicação de matrizes não seja comutativa, os determinantes de AB e BA são sempre iguais (se A e B são matrizes quadradas de dimensões iguais). Veja o artigo sobre determinantes para esclarecimento.
  • O produto é associativo, ou seja:
\left(AB\right)C=A\left(BC\right)\,
  • O produto distribui sob a soma:
\left(A+B\right)C=AC+BC\,
C\left(A+B\right)=CA+CB\,
Postado por às Nenhum comentário:

Regra de Cramer

A regra de Cramer é um teorema em álgebra linear, que dá a solução de um sistema de equações lineares em termos de determinantes. Recebe este nome em homenagem a Gabriel Cramer (1704 - 1752).
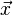Se A \vec x= \vec b é um sistema de equações. (A é a matriz de coeficientes do sistema, \vec x é o vetor coluna das incógnitas e 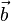\vec b é o vetor coluna os termos independentes)
Então a solução ao sistema se apresenta assim:
x_j = {\left| A_j \right| \over \left| A \right|}
Em que Aj é a matriz que se obtém da matriz A substituindo a coluna j pela coluna dos termos independentes b.

Demonstração

Sejam:
\vec x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}; A = \begin{bmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{n1} & \cdots & a_{nn}\end{bmatrix}; \vec b = \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}
A_j = \begin{bmatrix} a_{11} & \cdots & a_{1j-1} & b_1 & a_{1j+1} & \cdots & a_{1n} \\ a_{21} & \ddots & & & & & \vdots \\ \vdots & & \ddots & & & & \vdots \\ \vdots & & & \ddots & & & \vdots \\ \vdots & & & & \ddots & & \vdots \\ \vdots & & & & & \ddots & a_{n-1n} \\ a_{n1} & \cdots & a_{nj-1} & b_n & a_{nj+1} & \cdots & a_{nn}\end{bmatrix}
Usando as propriedades da multiplicação de matrizes:
A \vec x = \vec b \Leftrightarrow A^{-1} A \vec x = A^{-1} \vec b \Leftrightarrow I \vec x = A^{-1} \vec b \Leftrightarrow \vec x = A^{-1} \vec b
então:
\vec x = A^{-1} \vec b = \frac{(\operatorname{Adj} A)}{\left| A \right|} \vec b
Sejam:
A^{-1} \vec b = p_{jk}
(\operatorname{Adj}A) = \frac{A^\prime_{pl}}{A^\prime_{pl}} = A_{lp}
Portanto:
A^{-1} \vec b = p_{jk} = \sum_{i=1}^n \frac{A^\prime_{ji}}{\left| A \right|} b_{ik} = \frac{\sum_{i=1}^n A_{ij} b_i }{\left| A \right|} =_{\rm (1)} {\left| A_j \right| \over \left| A \right|}
(1) Recordando a definição de determinante, o somatório definido acumula a multiplicação do elemento adjunto o cofator da posição ij, com o elemento i-ésimo do vetor B (que é precisamente o elemento i-ésimo da coluna j, na matriz Aj

Exemplo

Um bom exemplo é a resolução de um simples sistema de equações 2x2:
Dado
ax+by = e\,
cx+dy = f\,
que em forma matricial é:
\begin{bmatrix} a & b \\ c & d \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} e \\ f \end{bmatrix}
x e y podem ser resultados usando a regra de Cramer
x = \frac { \begin{vmatrix} e & b \\ f & d \end{vmatrix} } { \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = { ed - bf \over ad - bc}
y = \frac { \begin{vmatrix} a & e \\ c & f \end{vmatrix} } { \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = { af - ec \over ad - bc}
Postado por às Nenhum comentário:
Assinar: Comentários (Atom)