Em matemática, o produto de duas
matrizes é definido somente quando o número de colunas da primeira matriz é igual ao número de linhas da segunda matriz. Se
A é uma matriz
m-por-
n e
B é uma matriz
n-por-
p, então seu
produto é uma matriz
m-por-
p definida como
AB (ou por
A ·
B). O produto é dado por

para cada par
i e
j com 1 ≤
i ≤
m e 1 ≤
j ≤
p.
Calculando directamente a partir da definição
A figura à esquerda mostra como calcular o elemento (1,2) e o elemento (3,3) de
AB se
A é uma
matriz 4×2, e
B é uma matriz 2×3. Elementos de cada matriz são postos par a par na direcção das setas; cada par é multiplicado e os produtos são somados. A posição do número resultante em
AB corresponde ao da seta e coluna que foi considerada.
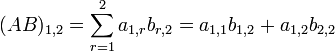

Propriedades
- Multiplicação de matrizes não é em geral comutativa, ou seja, AB ≠ BA(exceto em casos especiais). Eis um contra-exemplo:
![\left[\begin{array}{cc}
1 & 0 \\
0 & 2
\end{array}\right]
\cdot
\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]=
\left[\begin{array}{cc}
0 & 1 \\
2 & 0
\end{array}\right]](http://upload.wikimedia.org/math/6/d/0/6d02094418b33ca5b3ca492935f01cdb.png)
![\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]
\cdot
\left[\begin{array}{cc}
1 & 0 \\
0 & 2
\end{array}\right]=
\left[\begin{array}{cc}
0 & 2 \\
1 & 0
\end{array}\right]](http://upload.wikimedia.org/math/f/4/a/f4a335685523b3834dddc34a00b713ce.png)
- Embora multiplicação de matrizes não seja comutativa, os determinantes de AB e BA são sempre iguais (se A e B são matrizes quadradas de dimensões iguais). Veja o artigo sobre determinantes para esclarecimento.
- O produto é associativo, ou seja:

- O produto distribui sob a soma:




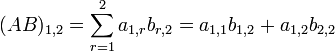

![\left[\begin{array}{cc}
1 & 0 \\
0 & 2
\end{array}\right]
\cdot
\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]=
\left[\begin{array}{cc}
0 & 1 \\
2 & 0
\end{array}\right]](http://upload.wikimedia.org/math/6/d/0/6d02094418b33ca5b3ca492935f01cdb.png)
![\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]
\cdot
\left[\begin{array}{cc}
1 & 0 \\
0 & 2
\end{array}\right]=
\left[\begin{array}{cc}
0 & 2 \\
1 & 0
\end{array}\right]](http://upload.wikimedia.org/math/f/4/a/f4a335685523b3834dddc34a00b713ce.png)




Nenhum comentário:
Postar um comentário