Sistema de Equações Lineares

Um sistema de equações lineares (abreviadamente, sistema linear) é um conjunto finito de equações lineares nas mesmas variáveis.
Em matemática, a teoria de sistemas lineares é um ramo da álgebra linear, uma matéria que é fundamental para a matemática moderna. Algoritmos computacionais para achar soluções são uma parte importante da álgebra linear numérica, e tais métodos têm uma grande importância na engenharia, física, química, ciência da computação e economia. Um sistema de equações não-lineares freqüentemente pode ser aproximado para um sistema linear, uma técnica útil quando se está fazendo um modelo matemático ou simulação computadorizada de sistemas complexos.

Técnicas de resolução

Existem vários métodos equivalentes de resolução de sistemas.

Método da substituição

O método da substituição consiste em isolar uma incógnita em qualquer uma das equações, obtendo igualdade com um polinômio. Então deve-se substituir essa mesma incógnita em outra das equações pelo polinômio ao qual ela foi igualada.

Sistemas com duas equações

Um sistema com duas equações lineares se apresenta por: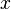

Onde e são as incógnitas.
Para solucioná-lo por substituição, substituem-se as variáveis em suas equações por seus polinômios correspondentes:

Portanto:

Método da soma

O método da soma é o mais direto para se resolverem os sistemas, pois é uma forma simplificada de usar o método da substituição. Só é possível quando as equações são dispostas de forma que, ao subtrair ou somar os polinômios das equações, todas as incógnitas, exceto uma, se anulam. É mais simples e direto que o outro método.

Sistemas com duas equações

Para solucionar um sistema como o apresentado a seguir por soma, onde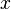 e são as incógnitas, deve-se subtrair os polinômios das equações.

O método da soma é possível apenas com determinadas incógnitas, dependendo das equações do sistema. Nesse caso, é possível apenas com uma. A outra deve ser determinada substituindo o valor descoberto para a primeira incógnita em uma das equações do sistema.

Método da comparação

Consiste em compararmos as duas equações do sistema, após termos isolado a mesma variável (x ou y) nas duas equações.

Fatorizações de matrizes

Os métodos mais utilizados computacionalmente para resolver sistemas lineares envolvem fatorizações de matrizes. O mais conhecido, a eliminação de Gauss, origina a fatorização LU. Resolver o sistema Ax=b é equivalente a resolver os sistemas mais simples Ly=b e Ux=6.

Regra de Cramer

A Regra de Cramer é um método resolver sistemas lineares utilizando determinantes.
Considere o sistema:

ax + by = e cx + dy = f

Pela regra de Cramer:

x =	Dx
	D

Em que Dx é o determinante da matriz dos termos do sistema excluindo a linha dos coeficientes de x, e D é o determinante da matriz dos coeficientes das incógnitas.

Dx =

b   e d   f

D =

a   b c   d

Para calcular o y basta trocar o Dx pelo Dy, que deve ser calculado da mesma forma, calculando o determinante da matriz dos termos do sistema excluindo a linha dos coeficientes de y.
Esse método serve para sistemas de qualquer tamanho, desde que o numero de incógnitas seja igual ao numero de equações. E muitas vezes esse método se mostra o caminho mais facil para solução de um sistema.