Casos particulares do Binómio de Newton são:
Notação e fórmula
O teorema do binômio de Newton se escreve como segue: são chamados coeficientes binomiais e são definidos como:
são chamados coeficientes binomiais e são definidos como: , onde
, onde  e
e  são inteiros,
são inteiros,  e
e  é o fatorial de x.
é o fatorial de x.
 corresponde, em análise combinatória, ao número combinações de n elementos agrupados k a k.
corresponde, em análise combinatória, ao número combinações de n elementos agrupados k a k.O triângulo de Pascal
Um algoritmo simples para calcular os coeficientes binomiais é o triângulo de Pascal.O triângulo de Pascal é um triângulo numérico infinito formado por coeficientes binomiais
 , onde
, onde  representa o número da linha (posição vertical) e
representa o número da linha (posição vertical) e  representa o número da coluna (posição horizontal).
representa o número da coluna (posição horizontal).A construção do triângulo faz-se de forma que cada elemento do triângulo de Pascal seja igual à soma dos elementos imediatamente acima e à direita com o elemento imediatamente acima e à esquerda. O elemento da primeira linha e primeira coluna é 1.
O príncipio do triângulo de Pascal é a relação de Stifel também conhecida como igualdade do triângulo de Pascal:
Por exemplo, o desenvolvimento de diversos binômios através dessa técnica:
Demonstração do teorema do Binômio de Newton
Antes de começar, vale lembrar que: (1)
(1)
-
- Base:
-
- Recorrência:
Da hipótese de indução:
Aplicações
O binómio de Newton pode ser usado para derivar diversas expressões matemáticas, através da escolha adequada de x e y. Por exemplo:


![1=[x+(1-x)]^n=\sum_{k=0}^n{n \choose k}x^k(1-x)^{n-k}=\sum_{k=0}^nB_k^n(x)](http://upload.wikimedia.org/math/0/2/9/0294ed9a3658b6c264a452ed5f8ccb50.png) , onde
, onde  são os polinómios de Bernstein.
são os polinómios de Bernstein.
- Recomendado:









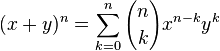

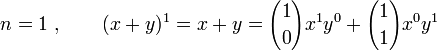







Nenhum comentário:
Postar um comentário