Um complexo na sua forma algébrica z = a + bi, possuindo parte real a e parte imaginária b
Desta forma um número complexo(z = a + bi) pode ser interpretado como um ponto no plano de Argand-Gauss, aonde pode ser trabalhado da mesma forma que no plano cartesiano, tendo seus afixos(pontos (x,y)) em a como x e b como y.
Um complexo pode ter associado nele um vetor de origem na origem(0,0) e extremidade em (a,b).
Na figura ao lado direito, o ponto no circulo é o afixo de z com as coordenadas (a,b).
O Módulo por definição é a distancia de um ponto até a origem, assim sendo o módulo do complexo z representado por |z| pode ser deduzido através da geometria analítica
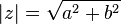 .
.O angulo Θ(Theta) que é medido a partir eixo x positivo, seguindo em sentido anti-horário, é chamado de argumento de um complexo.
É possível calcular Θ através de relações trigonométricas. Sendo Z = a + bi,


Um complexo apresenta também além da forma algébrica, uma forma trigonométrica(também conhecida por forma polar): Z = | z | (Cost + iSent) - Sendo t o angulo Theta(Θ) Por exemplo:



| z | = 2
Incompleto**


Nenhum comentário:
Postar um comentário