A
regra de Cramer é um
teorema em
álgebra linear, que dá a solução de um
sistema de equações lineares em termos de
determinantes. Recebe este nome em homenagem a
Gabriel Cramer (1704 - 1752).
Se

é um sistema de equações. (A é a
matriz de coeficientes do sistema,
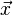
é o vetor coluna das incógnitas e
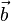
é o vetor coluna os termos independentes)
Então a solução ao sistema se apresenta assim:

Em que Aj é a matriz que se obtém da matriz A substituindo a coluna j pela coluna dos termos independentes b.
Demonstração
Sejam:


Usando as propriedades da
multiplicação de matrizes:

então:

Sejam:


Portanto:

(1) Recordando a definição de
determinante, o
somatório definido acumula a multiplicação do elemento adjunto o cofator da posição ij, com o elemento i-ésimo do vetor B (que é precisamente o elemento i-ésimo da coluna j, na matriz
Aj
Exemplo
Um bom exemplo é a resolução de um simples sistema de equações 2x2:
Dado


que em forma matricial é:

x e y podem ser resultados usando a regra de Cramer


 é um sistema de equações. (A é a matriz de coeficientes do sistema,
é um sistema de equações. (A é a matriz de coeficientes do sistema, 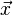 é o vetor coluna das incógnitas e
é o vetor coluna das incógnitas e 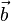 é o vetor coluna os termos independentes)
é o vetor coluna os termos independentes)














Nenhum comentário:
Postar um comentário