Viajando no mundo matemático: Função Trigonométrica

Em matemática, as funções trigonométricas são funções angulares, importantes no estudo dos triângulos e na modelação de fenómenos periódicos. Podem ser definidas como razões entre dois lados de um triângulo retângulo em função de um ângulo, ou, de forma mais geral, como razões de coordenadas de pontos no círculo unitário. Na análise matemática, estas funções recebem definições ainda mais gerais, na forma de séries infinitas ou como soluções para certas equações diferenciais. Neste último caso, as funções trigonométricas estão definidas não só para ângulos reais como também para ângulos complexos.
Atualmente, existem seis funções trigonométricas básicas em uso, cada uma com a sua abreviatura notacional padrão conforme tabela abaixo.
As inversas destas funções são chamadas de função de arco ou funções trigonométricas inversas. A nomenclatura é feita através do prefixo "arco-", ou seja, arco seno, arco co-seno, etc. Matematicamente, são designadas por "arcfunção", i.e., arcsen, arccos, etc.; ou adicionando-se o expoente −1 ao nome, como em $\operatorname{sen}^{-1}$ e $\operatorname{cos}^{-1}$ . O resultado da função inversa é o ângulo que corresponde ao parâmetro da função. Por exemplo, $\operatorname{arcsen}(1) = \frac{\pi}{2}$ , pois $\operatorname{sen}\,\frac{\pi}{2} = 1$ .

História

A noção de que existe alguma correspondência padrão entre os tamanhos dos lados de um triângulo e os ângulos do triângulo surge assim que se reconhece que triângulos semelhantes têm as mesmas razões entre seus lados. Isto é, para qualquer triângulo semelhante, a razão entre a hipotenusa (por exemplo) e um dos outros lados permanece a mesma. Se a hipotenusa for duas vezes maior, os lados serão duas vezes maiores. As funções trigonométricas expressam justamente tais razões. As funções trigonométricas foram estudadas por Hiparco de Nicéia (180-125 a.C.), Ptolomeu do Egito (90-165 d.C.), Aryabhata (476-550), Varahamihira, Brahmagupta, Muḥammad ibn Mūsā al-Ḵwārizmī, Abū al-Wafā' al-Būzjānī, Omar Khayyam, Bhāskara II, Nasir al-Din al-Tusi, Ghiyath al-Kashi (século XIV), Ulugh Beg (século XIV), Regiomontanus (1464), Rheticus, e o estudante de Rheticus, Valentin Otho.^{[carece de fontes?]}
Madhava de Sangamagramma (c. 1400) fez progressos iniciais na análise de funções trigonométricas em termos de séries infinitas.^[1] Introductio in analysin infinitorum (1748), de Leonhard Euler, foi em boa parte responsável por estabelecer o tratamento analítico das funções trigonométricas na Europa, também as definindo como séries infinitas e apresentando a "fórmula de Euler", bem como as abreviações quase modernas sin., cos., tang., cot., sec., e cosec.^[2]
Algumas funções eram historicamente comuns, mas agora são raramente usadas, como a corda (crd(θ) = 2 sen(θ/2)), o verseno (versen(θ) = 1 − cos(θ) = 2 sen²(θ/2)) (que surgiu nas mais antigas tabelas^[2]), o haverseno (haversen(θ) = versen(θ) / 2 = sen²(θ/2)), a exsecante (exsec(θ) = sec(θ) − 1) e a excossecante (excsc(θ) = exsec(π/2 − θ) = csc(θ) − 1). Muitas outras relações entre essas funções estão listadas no artigo sobre identidades trigonométricas.
Etimologicamente, a palavra seno deriva da palavra sânscrita para metade da corda, jya-ardha, abreviada para jiva. Esta foi transliterada para o árabe como jiba, escrita como jb, já que as vogais não são escritas em árabe. A seguir, a transliteração foi mal traduzida, no século XII, para o latim, como sinus, com a impressão errônea de que jb referia-se à palavra jaib, que significa "seio" em árabe, tal como sinus em latim.^[3] Finalmente, o uso em língua portuguesa converteu a palavra latina sinus para seno.^[4] A palavra tangente vem do latim tangens, que significa tocando, já que a linha toca o círculo unitário; já secante origina-se do latim secans — "cortando" — já que a linha corta o círculo.

Definição do triângulo retângulo

A fim de definir as funções trigométricas de um ângulo agudo não nulo $\alpha\,$ , considera-se um triângulo retângulo que possui um ângulo igual a $\alpha\,$ . As funções são definidas como:

Triângulo retângulo indicando a hipotenusa e os catetos.

$\begin{array}{rclcl} \sin \alpha &=& \frac{\hbox{cateto oposto}}{\hbox{hipotenusa}}&=&\frac{b}{h}\\ ~\\ \cos \alpha &=& \frac{\hbox{cateto adjacente}}{\hbox{hipotenusa}}&=&\frac{a}{h}\\ ~\\ \tan \alpha &=& \frac{\hbox{cateto oposto}}{\hbox{cateto adjacente}}&=&\frac{b}{a}\\ ~\\ \cot \alpha &=& \frac{\hbox{cateto adjacente}}{\hbox{cateto oposto}}&=&\frac{a}{b}\\ ~\\ \sec \alpha &=& \frac{\hbox{hipotenusa}}{\hbox{cateto adjacente}}&=&\frac{h}{a}\\ ~\\ \csc \alpha &=& \frac{\hbox{hipotenusa}}{\hbox{cateto oposto}}&=&\frac{h}{b} \end{array}\,$
Deve-se observar que as funções ficam assim bem definidas, ou seja, a relação entre os lados do triângulo não depende da escolha particular do triângulo, mas apenas dos ângulos do triângulo. Isto é uma conseqüência do teorema de Tales.

Definição no ciclo trigonométrico

A definição das funções trigonométricas pode ser generalizada para um ângulo $\theta\,$ real qualquer através do ciclo trigonométrico. O ciclo trigonométrico é um círculo de raio unitário centrado na origem de um sistema de coordenadas cartesianas. Como cada ponto $(x,y)\,$ pertencente ao ciclo está a uma distância 1 da origem, o teorema de Pitágoras afirma que:

$x^2 + y^2=1\quad (1)\,$

E, ainda, para cada ângulo $\theta\,$ existe um único ponto P pertencente ao círculo, tal que o segmento $\overline{OP}\,$ faz um ângulo $\theta\,$ com o eixo x.
Neste caso, o seno é definido como a projeção do segmento $\overline{OP}\,$ sobre o eixo y. O co-seno é definido como a projeção do segmento $\overline{OP}\,$ com o eixo x. Isto é:

$\sin\theta=y\quad \cos\theta=x\quad (2)\,$

As outras funções podem ser definidas conforme as relações a seguir:

$\begin{array}{rclrcl} \tan \theta &=& \frac{\sin \theta}{\cos \theta}\quad & \sec \theta &=& \frac{1}{\cos \theta}\\~\\ \csc\, \theta &=& \frac{1}{\sin \theta}\quad & \cot\, \theta &=& \frac{\cos \theta}{\sin \theta}\end{array}$

Deve-se observar que esta definição, quando restrita aos ângulos agudos, concorda com a definição no triângulo retângulo.

Relação fundamental

Observa-se diretamente de (1) e (2) a relação fundamental entre o co-seno e o seno de um ângulo $\theta\,$ :

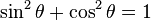
$\sin^2\theta+\cos^2\theta =1\,$

Definições geométricas

Alternativamente, todas as funções trigonométricas podem ser definidas geometricamente conforme figura ao lado. Observe que o triângulo OAE é retângulo, o cateto AO é unitário e o cateto AE é oposto ao ângulo $\theta\,$ e, portanto, sendo OE a hipotenusa deste triângulo, temos:

$\tan\theta=\frac{~~\overline{AE}~~}{\overline{AO}}=\overline{AE},\quad \sec\theta=\frac{~~\overline{OE}~~}{\overline{AO}}=\overline{OE}\,$

O triângulo AOF também é retângulo, sendo o cateto AO unitário, a hipotenusa OF e o ângulo AFO igual a $\theta\,$ , portanto:

$\cot\theta=\frac{~~\overline{AF}~~}{\overline{AO}}=\overline{AF},\quad \csc\theta=\frac{~~\overline{OF}~~}{\overline{AO}}=\overline{OF}\,$

Ângulos notáveis

Podemos calcular as funções trigonométricas para os ângulos de 30 e 60 graus através de um triângulo equilátero partido ao meio por sua altura.

$\begin{array}{rclcrcl} \sin 30^o &=& \frac{1/2}{1}=\frac{1}{2},\quad& \sin 60^o &=& \frac{\sqrt{3}/2}{1}=\frac{\sqrt{3}}{2}\\~\\ \cos 30^o &=& \frac{\sqrt{3}/2}{1}=\frac{\sqrt{3}}{2},& \cos 60^o &=& \frac{1/2}{1}=\frac{1}{2}\\~\\ \tan 30^o &=& \frac{1/2}{\sqrt{3}/2}=\frac{\sqrt{3}}{3},& \tan 60^o &=& \frac{\sqrt{3}/2}{1/2}=\sqrt{3}\\~\\ \cot 30^o &=& \frac{\sqrt{3}/2}{1/2}=\sqrt{3},& \cot 60^o &=& \frac{1/2}{\sqrt{3}/2}=\frac{\sqrt{3}}{3}\\~\\ \sec 30^o &=& \frac{1}{\sqrt{3}/2}=\frac{2\sqrt{3}}{3},& \sec 60^o &=& \frac{1}{1/2}=2\\~\\ \csc 30^o &=& \frac{1}{1/2}=2,& \csc 60^o &=& \frac{1}{\sqrt{3}/2}=\frac{2\sqrt{3}}{3} \end{array} \,$

As funções trigonométricas para o ângulo de 45 graus podem ser calculadas com o auxílio de um triângulo retângulo isósceles de catetos 1, cuja hipotenusa vale (pelo teorema de Pitágoras) $\sqrt{2}\,$ .

$\begin{array}{rclcrcl} \sin 45^o &=& \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2},\quad& \cos 45^o &=& \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\\~\\ \tan 45^o &=& \frac{1}{1}=1,\quad& \cot 45^o &=& \frac{1}{1}=1\\~\\ \sec 45^o &=& \frac{\sqrt{2}}{1}=\sqrt{2},\quad& \csc 45^o &=& \frac{\sqrt{2}}{1}=\sqrt{2} \end{array} \,$

Funções elementares

Função Seno

Gráfico de f(x) = sen x

f(x) = sen x

Associa a cada número real x o número $y = \operatorname{sen}\, x$

Domínio: Como x pode assumir qualquer valor real: $D = R$
Conjunto Imagem: Como seno possui valor máximo e mínimo, que são respectivamente 1 e -1, o conjunto imagem se encontra no intervalo entre esses valores: $\operatorname{Im} = [-1, 1]$
Gráfico: Ele sempre se repete no intervalo de 0 a $2π$ . Esse intervalo é denominado senóide. Para construir o gráfico basta escrever os pontos em que a função é nula, máxima e mínima no eixo cartesiano.
Período: É sempre o comprimento da senóide. No caso da função 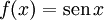$f(x) = \operatorname{sen}\, x$ , a senóide caracteríza-se pelo intervalo de 0 a $2π$ , portanto o período é 2 $π$ .
Sinal da Função: Como seno x é a ordenada do ponto-extremidade do arco:

f(x) = sen x é positiva no 1° e 2° quadrantes (ordenada positiva).
f(x) = sen x é negativa no 3° e 4° quadrantes (ordenada negativa).

Função Cosseno

f (x) = cos x

Associa a cada número real x o número

y = c o s x

Domínio: Como x pode assumir qualquer valor real: $D = R$
Conjunto Imagem: Como cosseno possui valor máximo e mínimo, que são respectivamente 1 e -1, o conjunto imagem se encontra no intervalo entre esses valores: $\operatorname{Im} = [-1, 1]$
Gráfico: Ele sempre se repete no intervalo de 0 a $2π$ . Esse intervalo é denominado cossenóide. Para construir o gráfico basta escrever os pontos em que a função é nula, máxima e mínima no eixo cartesiano.
Período: É sempre o comprimento da cossenóide. No caso da função f(x) = cos x , a cosenóide caracteríza-se pelo intervalo de 0 a $2π$ , portanto o período é $2π$ .
Sinal da Função: Como o cosseno x é a abscissa do ponto-extremidade do arco:

f(x) = cos x é positiva no 1° e 4° quadrante (abscissa positiva).
f(x) = cos x é negativa no 2° e 3° quadrante (abscissa negativa).

Função Tangente

Gráfico de f(x) = tg x

$f(x) = \operatorname{tg}\, x$

Domínio: A função da tangente apresenta uma peculiaridade. Ela não existe quando o valor de $cos x = 0$ (não existe divisão por zero), portanto o domínio são todos os números reais, exceto os que zeram o coseno.
Conjunto Imagem: $\operatorname{Im} = \left]-\infty, \infty \right[$
Gráfico: Tangentóide.
Período: $π$
Sinal da Função: Como tangente x é a ordenada do ponto T interseção da reta que passa pelo centro de uma circunferência trigonométrica e o ponto-extremidade do arco, com o eixo das tangentes então:

f(x) = tg x é positiva no 1° e 3° quadrantes (produto da ordenada pela abscissa positiva).
f(x) = tg x é negativa no 2° e 4° quadrantes (produto da ordenada pela abscissa negativa).

Definições analíticas

Funções trigonométricas: Verde - Co-seno, Azul - Seno, Vermelho - Tangente, Amarelo - Co-secante, Magenta - Secante, Ciano - Cotangente

Pode-se definir as funções $\operatorname{sen}(x)$ e

cos(x)

pelas séries de taylor a seguir:

$\operatorname{sen}(x)=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}x^{2n+1}$

$\cos(x)=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}x^{2n}$

Estas séries têm raio de convergência infinito e portanto definem as funções em todos os reais e também em todos os complexos.
As propriedades usuais destas funções podem ser inferidas diretamente das definições acima.

Soma de arcos

Sejam x e y quaisquer então:

$\operatorname{sen}(x+y)=\operatorname{sen}(x)\cos(y)+\operatorname{sen}(y)\cos(x)$

Dem.: $\operatorname{sen}(x+y)=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}(x+y)^{2n+1}$
Usando o binômio de Newton:

$\operatorname{sen}(x+y)=\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}\sum_{l=0}^{2n+1}{2n+1 \choose l}x^l y^{2n+1-l}$

A convergência uniforme nos permite rearanjar os termos:

$\operatorname{sen}(x+y)=\sum_{l\text{ ímpar}}x^l\sum_{n=(l-1)/2}^{\infty}\frac{(-1)^{n}}{(2n+1)!}{2n+1 \choose l}y^{2n}+\sum_{l\text{ par}}x^l\sum_{n=l/2}^{\infty}\frac{(-1)^{n}}{(2n+1)!}{2n+1 \choose l}y^{2n+1}$

$\operatorname{sen}(x+y)=\sum_{l\text{ impar}}x^l\sum_{n=(l-1)/2}^{\infty}\frac{(-1)^{n}}{l!(2n+1-l)!}y^{2n+1-l}+\sum_{l\text{ par}}x^l\sum_{n=l/2}^{\infty}\frac{(-1)^{n}}{l!(2n+1-l)!}y^{2n+1-l}$

Escreva (l=2i+1) no primeiro somatório e (l=2i) no segundo.

$\operatorname{sen}(x+y)=\sum_{i}^{\infty}x^{(2i+1)}\sum_{n=i}^{\infty}\frac{(-1)^{n}}{(2i+1)!(2n-2i)!}y^{2n-2i}+\sum_{i=0}^{\infty}x^{2i}\sum_{n=i}^{\infty}\frac{(-1)^{n}}{(2i)!(2n+1-2i)!}y^{2n-2i}$

Substitua $n \gets n+i$ :

$\operatorname{sen}(x+y)=\sum_{i}^{\infty}x^{(2i+1)}\sum_{n=0}^{\infty}\frac{(-1)^{n+i}}{(2i+1)!(2n)!}y^{2n}+\sum_{i=0}^{\infty}x^{2i}\sum_{n=0}^{\infty}\frac{(-1)^{n+i}}{(2i)!(2n+1)!}y^{2n}$

$\operatorname{sen}(x+y)=\left(\sum_{i}^{\infty}\frac{(-1)^i}{(2i+1)!}x^{(2i+1)}\right)\left(\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n)!}y^{2n}\right)+\left(\sum_{i=0}^{\infty}\frac{(-1)^i}{(2i)!}x^{2i}\right)\left(\sum_{n=0}^{\infty}\frac{(-1)^{n}}{(2n+1)!}y^{2n}\right)$

E assim: $\operatorname{sen}(x+y)=\operatorname{sen}(x)\cos(y)+\operatorname{sen}(y)\cos(x)$

domingo, 14 de fevereiro de 2010

Função Trigonométrica